I believe in the Socratic style of teaching. This pedagogical approach, rooted in interaction and critical thinking, emphasizes the learner’s active engagement in the process of learning. By posing thoughtful questions, there is ample opportunity to encourage students to reflect, analyze, and ultimately find the answers themselves.
However, despite the efficacy of the Socratic method, competitive educational environments often leave little room for such interactive learning. The coaching industry, with its emphasis on rapid problem-solving and performance, prioritizes providing students with quick fixes and handy formulas rather than guiding them toward discovering solutions themselves. As a JEE coach (I hesitate to call myself a teacher in this context), I’ve found myself caught in this cycle of offering solutions to students’ doubts1, which runs contrary to the principles of Socratic teaching. This practice becomes a repetitive exercise. Jumping from one student’s doubt to the next, I often find myself hurriedly solving problems without engaging in meaningful dialogue. This constant context-switching leads to errors—sometimes significant ones!
This article discusses my mistakes and attempts to explain why they occur.
Asking students to describe how they tackled the problems and where they ran into difficulties is missing in current coaching culture. In result, students are growing into a passive information consumers.
Doubt Solving Counter
Let me describe my everyday situation. As a JEE coach (Math SL, as designated by the institute), I deliver 5-6 periods of active teaching lectures, during which I must strictly follow the micro-schedule provided by the institute prior to the start of the session. This leaves little room for incorporating my own creativity into the lectures. It’s more about covering the topic rather than uncovering or discovering it together with the students. In addition to the 6 hours of lectures, there is a 2-3 hour doubt-clearing session (referred to as a counseling session), where students come with their doubts in a haphazard manner, as they try to finish as many questions as possible before the weekend test. These doubt sessions often turn into a abuzz gathering of students from different batches, each bringing different questions from various topics. I feel more like a solve-keeper sitting behind my doubt-clearing counter, haggling my solutions in the exchange of trivial questions. As a result, students often passively absorb the solutions I provide, and my teaching of problem-solving becomes superficial. Interaction is lacking. Focus drifts. Errors creep in.

The Rhombus Mistaken
One nice evening, I was at my doubt-clearing counter, solving a question from integral calculus. Then, the following question slipped in:
Q. The joint equation of two adjacent sides of a rhombus is \(7x^2 + 8xy + y^2 = 0 \). Find the slope of the longest diagonal of the rhombus.
Recognizing the urgency of the suddenly slipped-in query, I quickly guided the concerned students, at the desk, through the remaining steps of the integration problem and turned to the new question. Although traces of the previous question were still lingering in my mind, I began solving the new one. I tried to be as Socratic as possible, and the dialogue began.
Me: We can use the joint-bisector formula: \(\frac{x^2 – y^2}{a – b} = \frac{xy}{h}\) , and find each bisector equation by decomposing the given equation. The longer diagonal can be identified by drawing the diagram.
A student: Is there any other method?
Me: Let me think. [Pause] Since the equation \(7x^2 + 8xy + y^2 = 0\) can be decomposed into two equations of straight lines, \(y + 7x = 0\) and \(y + x = 0\), each passing through the origin, the diagram of the problem looks like this:
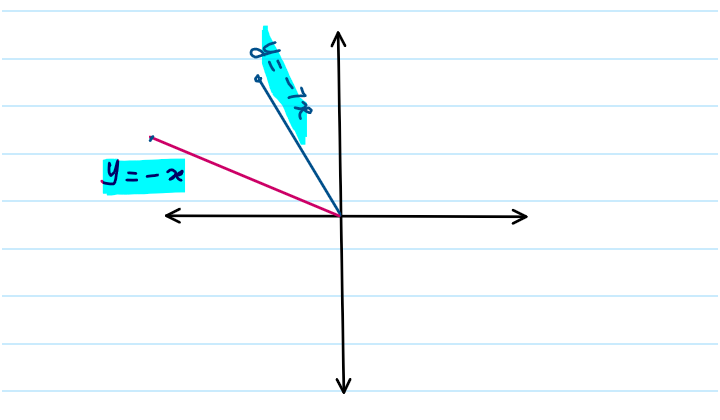
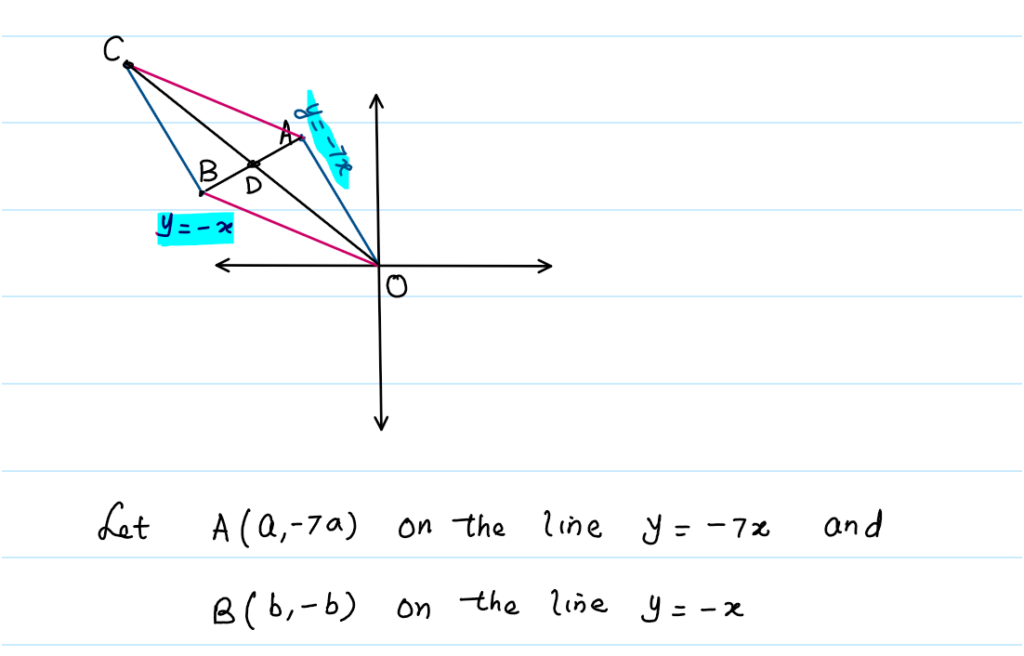
Now, take a general point on both lines, say A(a, -7a) and B(b, -b), respectively. Complete the rhombus, and you will get a diagram like this.
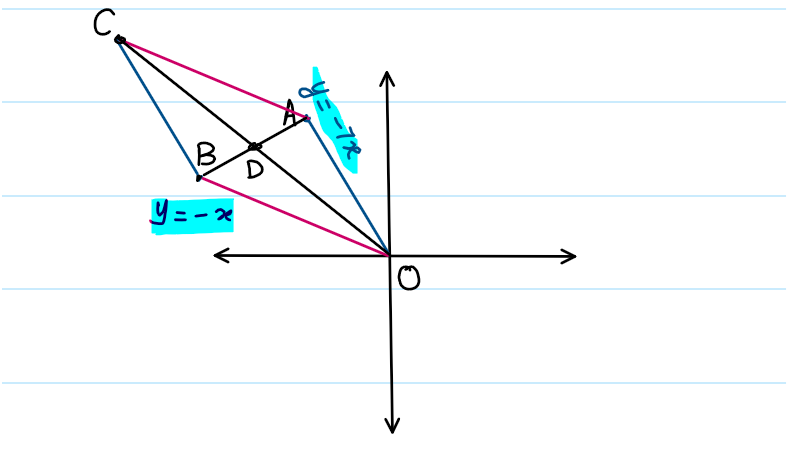
Students: After this, we can find the equations of BC and AC, use the midpoints of both diagonals, and locate point D. This way, we can find the slope.
Me: But, the diagonals of a rhombus do NOT bisect each other. So, I believe you should think more on it or apply the first method.
They left, and I moved on to a fresh question on determinants, with the residue of two half-solved problems still nagging in my mind—until about a minute later, when I realized the crime I had committed.
“I noticed I had said something wrong about the rhombus diagonals. In fact, the diagonal of rhombus bisect each other. How can I do such a mistake! What I meant to say was that the diagonal-midpoint idea wouldn’t work in this situation, as the diagonals of any parallelogram bisect each other. Therefore, BC and AC must be specific to confirm a rhombus, not just any two sides of any parallelogram.”
But the error had already been made. I was both amused and reflective. I knew this had happened due to the sudden shift from one task to another—what is known as attention residue.
Attention Residue
Attention residue is a phenomenon where thoughts about a previous task linger in the mind even after you’ve moved on to the next task. This occurs when there is insufficient transition time between completing one task and starting another, leading to a cognitive overlap. As a result, part of your focus remains with the previous task, making it harder to fully engage with the current one. In 2009, Dr. Sophie Leroy introduced the concept of attention residue in her research (original paper), highlighting the challenge of managing cognitive shifts. I first encountered this idea while listening to Cal Newport. Becoming more aware of this issue can lead to conscious steps toward improving focus and efficiency.
To focus on the present, you must first release what has already passed.
An Uncluttered Doubt-Clearing Session
In order to promote meaningful involvement and lessen stress for both the teacher and the students, an “Uncluttered Doubt-Clearing Session” is the need of the time. This is how I imagine such a session:
- Scheduled Time Slots: Instead of allowing students come in with questions at random, we may set up time slots for each student or small group, making sure that each question receives the proper amount of attention without being rushed through.
- Pre-Submission of Doubts: We may ask students to submit their doubts prior to the session. It saves time and saves redundancy by combining related questions into one group and addressing common issues all at once.
- Devoted Batch Sessions: We may have distinct doubt-clearing sessions based on batch or topic rather than combining students from multiple batches with different topics. As a result, all students will be able to gain from hearing one other’s queries.
In an ideal session, the emphasis would move from completing problems quickly to deeper comprehension and involvement, which would help students improve their critical thinking and problem-solving abilities.
To build a more richer learning environment, we must seek ways to include Socratic style of teaching even in fast-paced educational situations, ensuring that students are not merely passive recipients of knowledge, but active participants in their own intellectual development.
Solutions to the Question
Let’s now see how the question can be solved. Without keeping any attention residue, I arrived at two solutions to it.
Q. The joint equation of two adjacent sides of a rhombus is \(7x^2 + 8xy + y^2 = 0 \). Find the slope of the longest diagonal of the rhombus.
Solution 1: Using the combined-bisector equation of a pair straight lines.

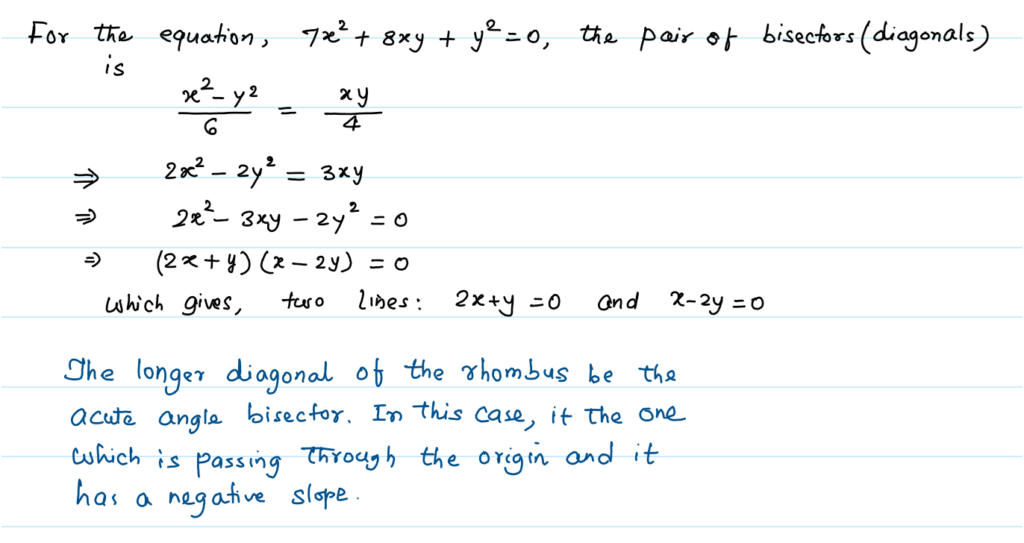
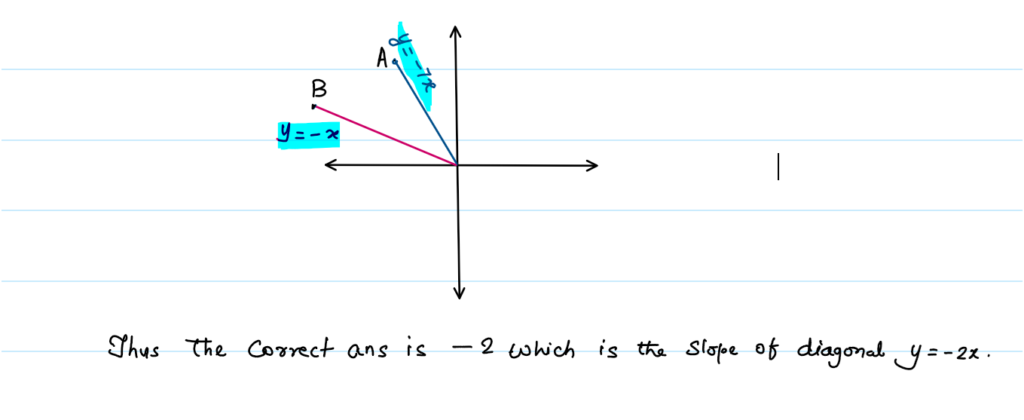
Solution 2: By Decomposing the Equation, and applying the property of rhombus.
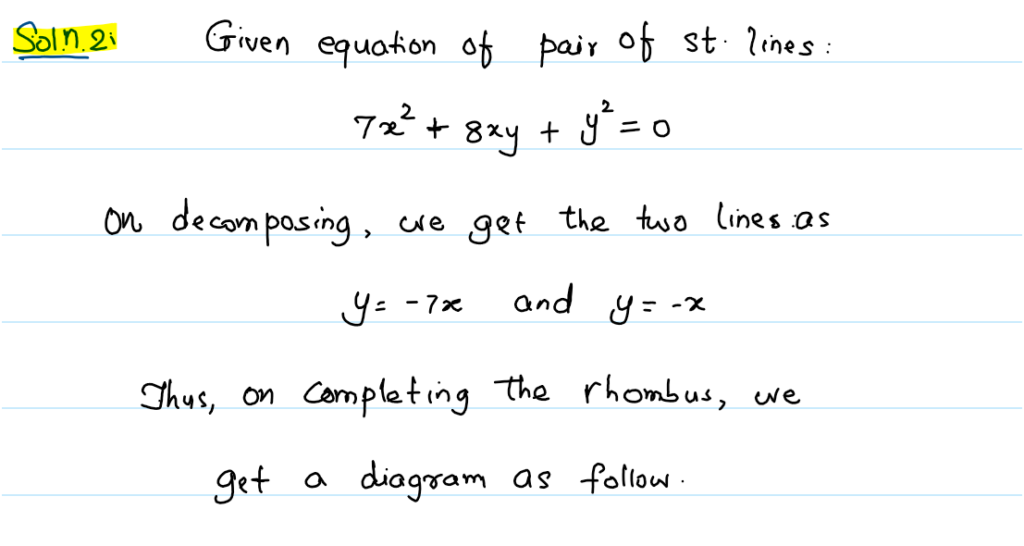
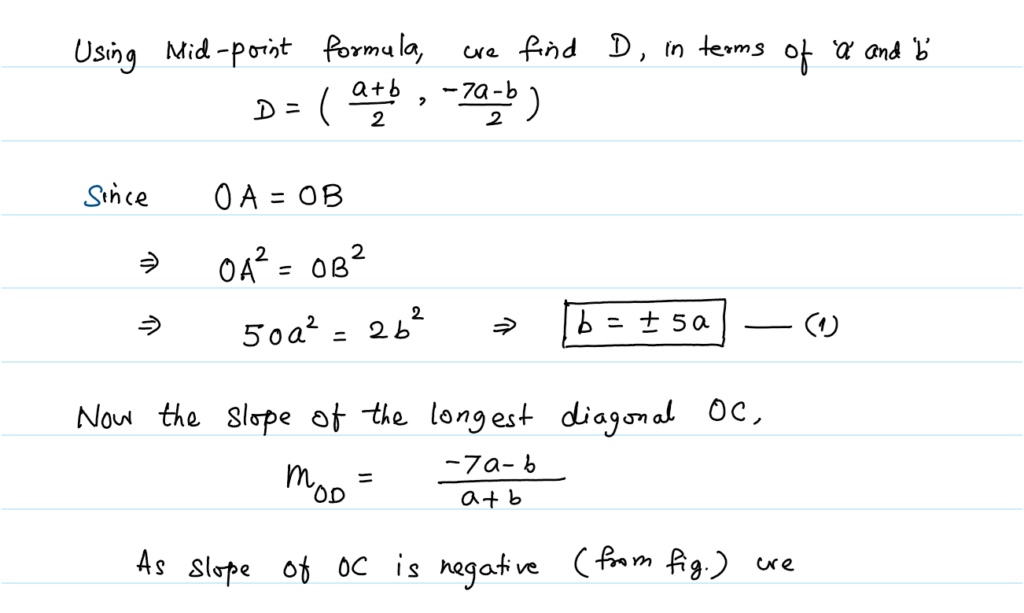
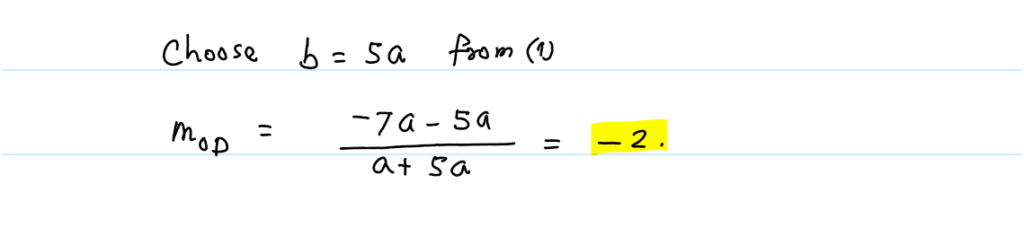
- doubts: a query, a question in Indian Context. In fact, The word “doubt” generally refers to a feeling of uncertainty or lack of confidence about something. It can also mean questioning the truth or validity of something. ↩︎


1 thought on “Rhombus, Attention Residue, Doubts: A Teacher’s Dilemma”
Attractive section of content I just stumbled upon your blog and in accession capital to assert that I get actually enjoyed account your blog posts